I recently saw one of several “Deep Zoom” videos of the Mandelbrot set, which I’ll leave alone for now, but it got me interested in the subject, which I haven’t thought about since the 1980’s. Times change, and the facilities available for investigating the subject are now, of course, much more powerful. I looked at the Wikipedia article on the Mandelbrot set, which refreshed and greatly expanded my casual knowledge of the subject. The exciting thing though is the link under the section headed “Image gallery of a zoom sequence” to an “interactive viewer” ( go to Wikipedia to get the link. ) It indicates it will open for “this location” ( i.e. the one illustrated ) but I found it goes to the initial full view of the set.
Anyway, it’s a fabulous tool. You can click on a spot to zoom by a factor of two, and although it does take time to calculate the image, you can click again for repeated zooms without waiting for the full resolution. I found it very handy to use. It goes down to 10^-14 in scale, which is well short of the claims made by these deep zoom videos, but it provides ample scope for casual exploration.
Note the parameters are passed in the URL address field, and these can be edited and entered with the naturally hoped for result. Of course you can save them and reenter them to bring back the image, so as I say, very handy.
I also used the extended precision calculator, bc, on Cygwin to explore some of the mathematical aspects, which I’ll get to. First, here’s an animated gif of a short zoom on a large portion of the Mandelbrot set, progressing down the scale of the circular “bulbs” along the real axis. This is a more extensive version of the “Mandelbrot zoom” gif in the Wiki article which uses a loop of two circles without “hair”.

First note that the Mandelbrot set itself is the black area, determined by points c, where the iteration of the defining formula always remains bounded. The “hair” is exterior to the set and is colored according to how rapidly the formula diverges under iteration.
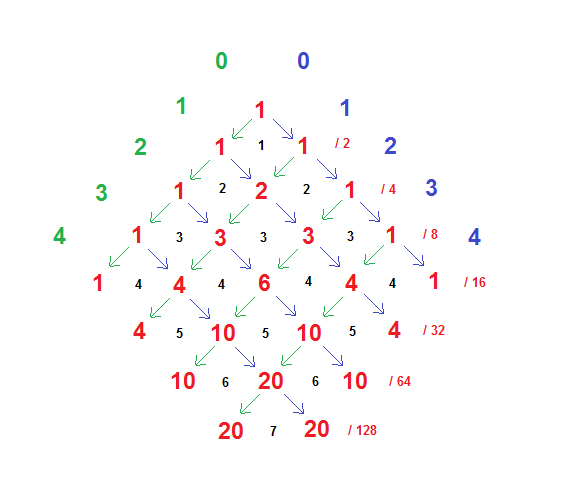
These circles are in the set, and are called “period bulbs” in the article, because of the defining nature of the points within them. That is, they are points c, in the imaginary plane, such that iteration of x = x^2+c ( where ‘=’ means assignment, as in a programming language ) starting with x == 0 ( ‘==’ asserts equality ) converges to a cycle of fixed values, these values being 2 in number in the “2” bulb ( the first circle ) then 4 in number, then 8, 16, 32, and 64 in number in the large circle of the sixth and last frame.
This brings us to the math, and bc. Let’s go for the gusto with the “64 bulb”. Using the “click and zoom” facility in the interactive viewer, we go to the sixth bulb, i.e. the 64 bulb, and simply copy and paste the x-axis ( i.e. real part ) value into bc, and initialize x to 0:
c= -1.400968738408754
x=0
Then we iterate for a goodly number of times to assure ourselves of convergence to a stable cycle, in the belief this must happen:
( Even though bc runs interpretively, the power of a modern PC is such that this number of iterations causes a barely perceptible hitch in the response )
n=100000
for( i=0 ; i<n ; i++ ) x=x^2+c;x
.010561399880314
Now we check for a 64 cycle of values:
n=64
for( i=0 ; i<n ; i++ ) x=x^2+c;x
.010561399880314
OK! But maybe this is a repetition of a shorter cycle, so check 32:
n=32
for( i=0 ; i<n ; i++ ) x=x^2+c;x
-.000137388541270
for( i=0 ; i<n ; i++ ) x=x^2+c;x
.010561399880314
OK again! We can now be satisfied that 64 is the true cycle value. Note that we didn’t use a lot of precision, but the “attractive cycle” is strong medicine, and we don’t need it. We are just checking the fundamentals though, and of course there are more delicate arrangements to be found.
In particular, what about the “vanishing point” of this self-similarity? It is cited in the article to crude precision as -1.401155, which can be discerned numerically, but what are its defining properties? This point remains obscure to me.
Misiurewicz points
These are defined as values of c such that k iterations of x=x^2+c give a value that repeats after n ( more ) iterations, and are designated as M_k,n, and these form vanishing points for self-similar transformations although they do not account for the seemingly fundamental one just described. Noteworthy is M_4,1 described in the Wiki article.
Here is a zoom which goes by steps of 100X magnification ( after an initial step of 10X ) 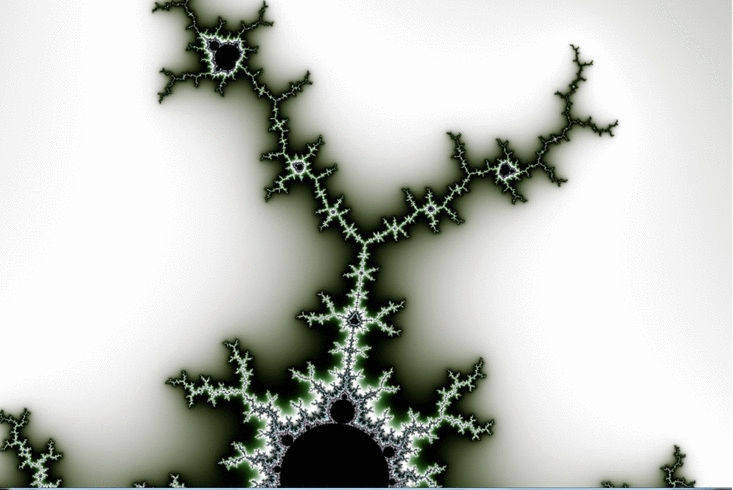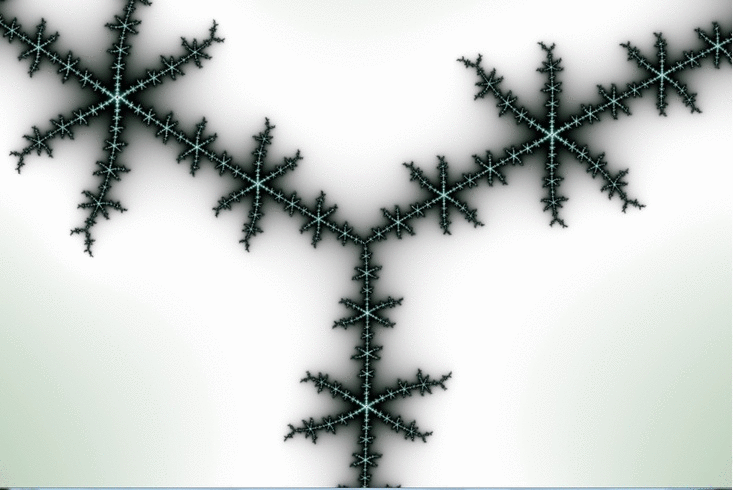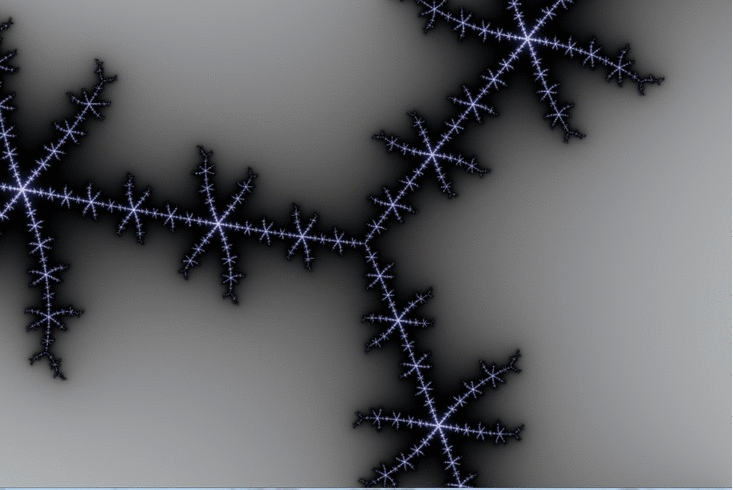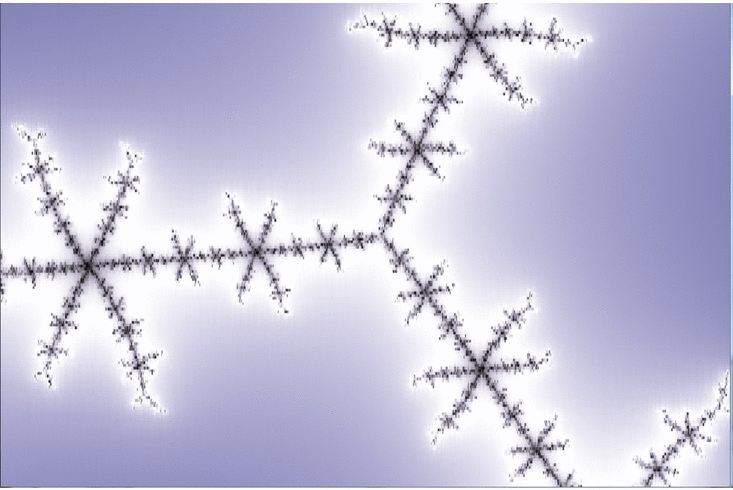
The Wikipedia article on Misiurewicz points mentions … “(Even the `principal Misiurewicz point in the 1/3-limb’, at the end of the parameter rays at angles 9/56, 11/56, and 15/56, turns out to be asymptotically a spiral, with infinitely many turns, even though this is hard to see without maginification.)” ( sic ! just noticed that. ) … This is our guy, and you can see the “slow roll”, which advances by about 50 degrees in 6 steps of 100X magnification. ( I’m still working on the meaning of those angle values. )
In this case we can do a little math and come up with a way to define the M_4,1 point, at the center of the zoom, to arbitrary precision. Approaching it graphically we see the center at approximately ( -.10109636 , .95628651 ) in the complex plane.
In bc we define functions:
define f(a,b){ return( a^2-b^2 + c); }
define g(a,b){ return( 2*a*b +d ) ; }
… which are the real and imaginary parts of the formula, x^2 + (c,d) , applied to a complex value x with real and imaginary parts (a,b) . So we can proceed to apply the formula iteratively and see if we come up with a constant value after 4 iterations, as per the M_4,1 designation:
c= -.10109636
d= .95628651
x=y=0
z=f(x,y);y=g(x,y);x=z;x;y # iteration 1
-.10109636
.95628651
z=f(x,y);y=g(x,y);x=z;x;y # iteration 2
-1.0053597752027305
.7629323394437928
z=f(x,y);y=g(x,y);x=z;x;y # iteration 3
.32758616302650612570470420629841
-.57775646055620961839245967248080
z=f(x,y);y=g(x,y);x=z;x;y # iteration 4
-.32758619350801035155822390304043175425331545129536
.57775646584523271983382407623684575759993010598581
z=f(x,y);y=g(x,y);x=z;x;y # iteration 5
-.32758617964890595894029463234712218921204878613363
.57775642715823884156305664636678518208809205705010
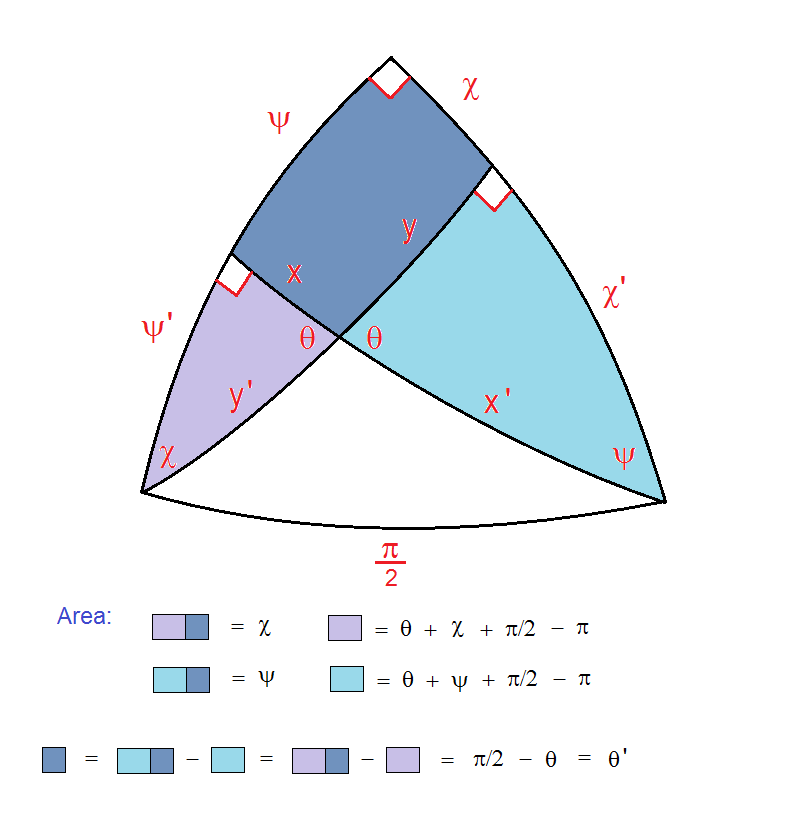
Note that the 4th iteration approximately achieves the repeated value, but the 3rd iteration is the negative of it. So to home in on the exact value we want to adjust c so that f(f(f(f(0)))) = – f(f(f(0))). Without spelling it all out, we can do this by numerically evaluating the sum of the 3rd and 4th iterate ( which we want to be 0 ) to see how it varies with small variation in the real and imaginary parts of c . This is essentialy “Newton’s method” of finding roots. Inverting a simple 2X2 matrix tells how to vary ( c, d ) to bring this sum to 0. By iterating this estimation we can find the correct complex value of M_4,1 to arbitrary precision.
Here’s as far as I’ve taken it so far:
( c, d ) = (
#real part
-.1010963638456221610257854457386225654638054428262534
838769311776607808407404705842748212198105167791
,
# imaginary part
.9562865108091415007710960577299774358098333365105291
700343143215005246590657167325269784107873398073
)
It’s very easy to do and could be taken to many thousands of decimal places in less than an hour, I’m sure.
I’ve got a lot more, but I want to put something out now and I do plan to continue my discussion … but let me just outline my thoughts.
The mathematical structure of the Mandelbrot set has been a matter of ongoing investigation, and is a difficult subject. One fundamental point is the “connectedness” of the set, and it has been proven that it is “connected” according to the literature. Well, I’m sure it has, but I still have questions! In particular it seems to me that these Misiurewicz points must be isolated elements of the set. Perhaps in some sense they are, since topology has more definitions than you can shake a stick at.
Anyway, I hope to be back with more pictures.








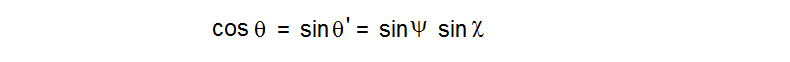
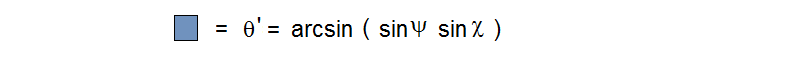
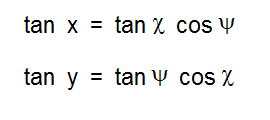



 ( To see its full glory visit the site. ) It roughly corresponds to the antepenultimate frame of the animated gif. The commentary in the main article notes that there is a “satellite” ( i.e. “mini-Mandelbrot set” ) at the center of the island structure that is “too small to see at this magnification”. Just visible there is the large square structure in the center of the last frame of the gif, where you can almost see the satellite at the center of it, as a tiny dark speck.
( To see its full glory visit the site. ) It roughly corresponds to the antepenultimate frame of the animated gif. The commentary in the main article notes that there is a “satellite” ( i.e. “mini-Mandelbrot set” ) at the center of the island structure that is “too small to see at this magnification”. Just visible there is the large square structure in the center of the last frame of the gif, where you can almost see the satellite at the center of it, as a tiny dark speck.




