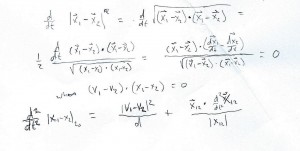I came across the Spot it! card game a few months ago, and it didn’t take long to start wondering about the mathematics of the deck design. Here is the game with three cards displayed. Every pair of cards has exactly one matching pair of symbols, as illustrated here where the three pairings share a chess knight, a cat, and a dog.
 There are 8 cards that have knights on them, and a little consideration shows that the 8×7 other symbols on these cards must be unique ( since each pair of cards has one match. ) Then there must be 57 symbols, on this fact alone. If there are 57 cards, then each of the 57 symbols can be accounted for if they each appear on 8 cards.
There are 8 cards that have knights on them, and a little consideration shows that the 8×7 other symbols on these cards must be unique ( since each pair of cards has one match. ) Then there must be 57 symbols, on this fact alone. If there are 57 cards, then each of the 57 symbols can be accounted for if they each appear on 8 cards.
I got this far, then found the blog, BOWMAN IN ARABIA with the article, Math Circle Problem: Analysis of the Game “Spot it!”, which outlines an algorithm for finding decks of PX(P+1) + 1 cards and the same number of unique symbols, with P+1 symbols on each card, for P prime.
I added a note about a solution for P=4, and I surmised that P = 2N works along with P prime. I wrote ( and refined, with considerable effort, ) a “brute force” search program, and verified that P=6 does not yield a solution, and proceeded to P=9, expecting the same. However, this search yielded numerous solutions. ( I let it run for several days, thinking that it would stop at 7! solutions, based on simple extrapolation. However, it was still going strong at that point and I terminated the run. ) I then surmised that PN + 1, P prime, yields solutions, and this seems to be corroborated from what I read, and is evidently related to the “Sylow subgroups” of the Symmetric groups (aka permutation groups. )
You could say that’s the end of it, but there are a lot of “pfathinatin” details to be observed in the structure and properties of these solutions. Let us first return to the commercially available SPOT IT! deck, and then consider some other simple cases.
In fact, there are 55 cards in this deck, and it is observed that it must be obtained simply by removing two cards from the mathematically ideal solution. This is verified by the following image of a canonical arrangement of the cards, with the two “missing” cards ( they are not there when you buy them! ) … supplied by the logic explained:
 On the left is the arbitrarily chosen ABCDEFGH card, whose 8 symbols are given canonical status. Note that in each of the 8 rows of 7 cards, each card contains the same symbol from the “key card” , with A=knight, B=balloon, etc. ( The “key symbol” is given upright orientation in each case. )
On the left is the arbitrarily chosen ABCDEFGH card, whose 8 symbols are given canonical status. Note that in each of the 8 rows of 7 cards, each card contains the same symbol from the “key card” , with A=knight, B=balloon, etc. ( The “key symbol” is given upright orientation in each case. )
The top row defines 8 canonical sets of 7 symbols, ( excluding the knight, ) one of which must appear in each of the cards of every row. The second row, or “B=balloon” row, arranged in arbitrary order, defines a canonical index into each of these sets, based on the row position of its member symbols. This index is important in algorithms for constructing “solutions”, i.e. valid SPOT IT! decks.
Then … each subsequent row is arranged so that the symbols matching the left-top-most card, the second key card, are in the same order as the “B=balloon” row, thus forming a 7X7 array of cards, excluding only the “A=knight” cards, indexed in a canonical way by the seven non-knight symbols on the two key cards. Wonderful!
Well, note that we come up with two “holes” in a very natural way, and can fill them in according to the symbol missing in their row from each of the “A row” cards, and this has been done, at great cost of manual labor.
General Principles
But let us return to a simpler case to illustrate some general considerations. The very simplest nontrivial case is 3 ( 2X1 + 1 ) cards with 2 symbols on each card, AB, AC, BC. However, this is a bit too simple, and the next case of 7 ( 3X2+1) cards with 3 symbols on each card is interesting but not too complicated.
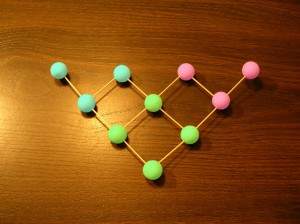
It suffices to illustrate the geometric model, where each card is a vertex of a 6-d simplex ( noting that a 3-d simplex has 4 vertices, e.g. ) and each symbol corresponds to a 2-d simplex, or triangle, connecting all of the vertices representing cards with the same matching symbol.
Thus, the whole problem of constructing a deck of N X (N+1)+1 cards is seen to be equivalent to an EDGE COLORING problem on an N X (N+1)-simplex. We require the edges to be colored ( in this case) with 7 colors, such that the edges of 7 2-simplexes ( triangles) have the same (unique) color, and each vertex is shared by 3 of these.
Not sure where that gets us, but it does seem to be a helpful visualization.
Duality
In consideration of the idealized SPOT IT! deck, it appears that just as every pair of cards shares a unique symbol, so every pair of symbols shares, or appears on, a unique card. Thus every deck can be specified in a dual fashion, with a solution that corresponds to itself or another deck.
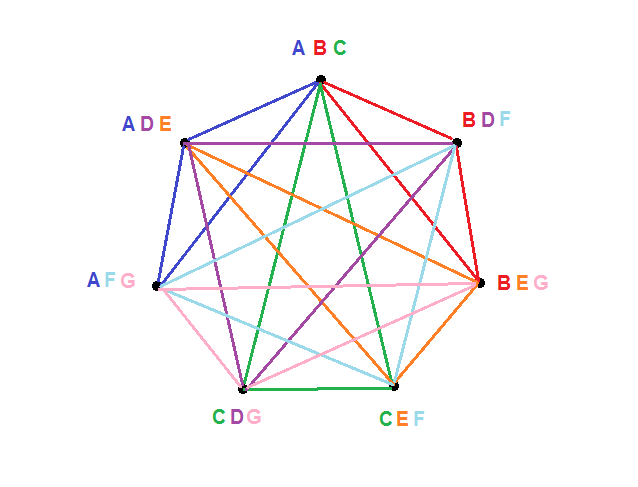
For the case of N=3 we can see a SELF-DUAL solution if we label each card with a,b,c,d,e,f,g as follows
a=ABC b=ADE c=AFG d=BDF e=BEG f=CDG g=CEF
… indicating which symbols occur on each card. Then the symbols can be specified by the set of cards on which they occur:
A=abc B=ade C=afg D=bdf E=beg F=cdg G=cef
… and we see that we have the same specification with interchange of upper and lower case. I promise you that I typed these out according to the definition, and not by rote! For higher values of N, the solutions are not all self-dual, and I haven’t explored the necessary arrangements.
Permutation of symbols
It seems clear that any solution derived by permuting the symbol values of an existing solution is valid, and will not necessarily involve the same cards, as defined by the symbols appearing on them. In the case of 7 symbols appearing 3 times each on 7 cards, we can easily permute them and “orthonormalize” them to arrive at the 7! = 5040 different results:
$ for i in `perm ABCDEFG`; do tr ABCDEFG $i <ABC | orsort; done | sort | uniq -c
168 ABC ADE AFG BDF BEG CDG CEF
168 ABC ADE AFG BDG BEF CDF CEG
168 ABC ADF AEG BDE BFG CDG CEF
168 ABC ADF AEG BDG BEF CDE CFG
168 ABC ADG AEF BDE BFG CDF CEG
168 ABC ADG AEF BDF BEG CDE CFG
168 ABD ACE AFG BCF BEG CDG DEF
168 ABD ACE AFG BCG BEF CDF DEG
168 ABD ACF AEG BCE BFG CDG DEF
168 ABD ACF AEG BCG BEF CDE DFG
168 ABD ACG AEF BCE BFG CDF DEG
168 ABD ACG AEF BCF BEG CDE DFG
168 ABE ACD AFG BCF BDG CEG DEF
168 ABE ACD AFG BCG BDF CEF DEG
168 ABE ACF ADG BCD BFG CEG DEF
168 ABE ACF ADG BCG BDF CDE EFG
168 ABE ACG ADF BCD BFG CEF DEG
168 ABE ACG ADF BCF BDG CDE EFG
168 ABF ACD AEG BCE BDG CFG DEF
168 ABF ACD AEG BCG BDE CEF DFG
168 ABF ACE ADG BCD BEG CFG DEF
168 ABF ACE ADG BCG BDE CDF EFG
168 ABF ACG ADE BCD BEG CEF DFG
168 ABF ACG ADE BCE BDG CDF EFG
168 ABG ACD AEF BCE BDF CFG DEG
168 ABG ACD AEF BCF BDE CEG DFG
168 ABG ACE ADF BCD BEF CFG DEG
168 ABG ACE ADF BCF BDE CDG EFG
168 ABG ACF ADE BCD BEF CEG DFG
168 ABG ACF ADE BCE BDF CDG EFG
… showing that the 5040 permutations of the symbol tags, ABCDEFG, result in 168 repetitions each of 30 different 7 card decks, each a solution of the SPOT IT! specification.
ABC is a file containing the original 7 card solution
$ cat ABC
ABC ADE AFG BDF BEG CDG CEF
This takes a minute to run on CYGWIN, even with todays mind-bogglingly fast processor speeds, because of the shell level logic. ( “perm” and “orsort” are C programs I wrote. ) So this is my excuse for not offering results for higher values of N.
Generating solutions
As I mentioned above, my first investigation of the SPOT IT! problem involved writing programs to generate solutions for small values of N, where N is the number of symbols on each card of a deck comprising N X ( N-1 ) + 1 cards. I led off this discussion with a canonical arrangement of the actual commercial SPOT IT! deck, which provides the framework for this effort, as noted.
The cards containing two symbols, designated A and B, can be specified in a canonical arrangement which labels all the available symbols, and the solution for a full deck entails specifying additional cards, each with N of these symbols on it, that complete the deck and satisfy the unique matching condition.
Here is the top portion of the image above with numerical indexes overlayed on the symbols, according to the scheme explained:
The symbols on the A row ( other than A=knight ) are labeled according to the position of their occurrence in the second ( B=balloon ) row, which is not labelled because every label corresponds to the position of the card, 1 thru 7. Each card of the A row is labelled with a different color, indicating its column.
The third, or C=zebra, row has each symbol labeled according to its color and value in the A row. It so happens that for this case of N=8, once the C row is specified, the solution is unique. Using the color to indicate a column, as noted, the labeling generates the array specification:
… and these are the terms in which my program generates solutions. That program found 120 unique solutions in these terms, of which this one happens to be the 14th:
1 2 3 4 5 6 7
2 3 6 1 7 5 4
3 6 5 2 4 7 1
4 1 2 7 6 3 5
5 7 4 6 2 1 3
6 5 7 3 1 4 2
7 4 1 5 3 2 6
1 3 5 7 2 4 6
2 6 7 4 3 1 5
3 5 4 1 6 2 7
4 2 6 5 1 7 3
5 4 2 3 7 6 1
6 7 1 2 5 3 4
7 1 3 6 4 5 2
1 4 7 2 6 5 3
2 1 4 3 5 7 6
3 2 1 6 7 4 5
4 7 5 1 3 6 2
5 6 3 7 1 2 4
6 3 2 5 4 1 7
7 5 6 4 2 3 1
1 5 2 6 3 7 4
2 7 3 5 6 4 1
3 4 6 7 5 1 2
4 6 1 3 2 5 7
5 2 7 1 4 3 6
6 1 5 4 7 2 3
7 3 4 2 1 6 5
1 6 4 5 7 3 2
2 5 1 7 4 6 3
3 7 2 4 1 5 6
4 3 7 6 5 2 1
5 1 6 2 3 4 7
6 4 3 1 2 7 5
7 2 5 3 6 1 4
1 7 6 3 4 2 5
2 4 5 6 1 3 7
3 1 7 5 2 6 4
4 5 3 2 7 1 6
5 3 1 4 6 7 2
6 2 4 7 3 5 1
7 6 2 1 5 4 3
The C row matches, and I spot checked the D, E, etc. rows, which according to my logic must necessarily match.
And now a true confession. Note that the C row array specification is symmetric about the major diagonal. I.e. we have 1, 22, 333, 4664, 51515, etc. reading from the left column up to the right, proceeding from top to bottom. I noticed that the solutions, starting from this canonical form and using brute force search, had this form for small N, up to N=5. I found that for N=8, e.g., the brute force search bogged down hopelessly, searching through fruitless combinations, so I restricted the search to these symmetrical C row arrays, and was able to proceed up to N=9. It rankles me, but I haven’t been able to prove that this condition is necessary, however evident it seems that it must be true.
Concomitant to the symmetric C row array, we see that the other row arrays are each formed by a permutation of the columns of index values into the canonically order sets of symbols defined by the A and B rows. This is a purely empirical observation, but it certainly seems to be true in general, and so I stand in perplexity.
More on enumeration of solutions
I commented above under the “Permutation of symbols” heading, that brute force enumeration, which I carried out for the case of 3 symbols per card, is not practical for larger values. Note that with 4 symbols per card we have 13 instead of 7 unique symbols, and 13! = 6227020800, as compared to 7! = 5040. However, some straightforward reasoning allows us to proceed.
Starting with the case of N=3 symbols per card, we can observe that we must have a unique ABx card, and there are then 5 choices for the third symbol, x, on that card, and each of these cases is equivalent, since the labelling of the symbols is arbitrary. Also every deck containing a different ABx card is different, so there are 5 equinumerous sets of unique decks, all different.
So it suffices to enumerate the decks containing an ABC card. We note there must be an AD card, which must be ADE, ADF, or ADG, and following the same reasoning as above, these define 3 equinumerous sets of unique decks, so now we have 15 sets of decks, each equinumerous with the deck containing ABC, ADE, and we can anticipate from the earlier enumeration of 30 unique 3 symbol decks that each of these sets has 2 unique decks.
So continuing, with ABC, ADE, we must have AFG, and we must have a BDx card, which can be BDE or BDG, so the two possible decks are :
ABC ADE AFG BDF BEG CDG CEF
ABC ADE AFG BDG BEF CDF CDG
… and we have 5*3*2 = 30 unique decks with 3 symbols on each card, given 7 unique symbols, so we move along to the case of N=4.
With 13 symbols, we see that there will be C(11,2) = 55 possible cards, ABxy, with the 11 remaining symbols taken in combination 2 at a time. Then in each case, using ABCD as our exemplar, we will have C(8,2) = 28 possible cards, AExy, and then C(5,2) = 10 AHxy cards, leaving the AKLM card, making 15400 unique sets of 4 Axyz cards. For each these sets, we can form the same number of Bxyz cards ( x,y,z != A ) so we take the case of { ABCD, AEFG, AHIJ, AKLM } and note that each Bxyz must have one symbol from each of the last 3 in this “A set” . There must be a BEyz, BFyz, and BGyz card, and there are 3!*3! ways to assign {H,I,J} and {K,L,M} to y and z. So there are 36 “B sets”.
Now we come to the point of the matrix solution which completes a deck given canonically chosen “A & B sets”, as described above for the case of N=8, the true SPOT IT! deck. One last factor to account for is the interchange of the remaining symbols after A and B. The matrix solution assumes a canonical order for these, so that it won’t redundantly find solutions obtained by shuffling the matrices around. For N=4 this just means a factor of 2 to allow for the swapping of C and D.
Then, in the case of N=4, we get the unique matrix solution:
1 2 3
2 3 1
3 1 2
1 3 2
2 1 3
3 2 1
Which just means that given
ABCD AEFG AHIJ AKLM BEHK BFIL BGJM CE.. CF.. CG.. DE.. DF.. DG..
there is a unique solution, “up to” interchange of C and D. Note that CE, CF, CG, DE, DF, DG must each be present, and this is accounted for in the matrix solution by setting the first column always to 1,2,3 as indexes to E,F,G in the second position of the “B cards” .
This brings us to N=8. The reasoning just adduced gives a general formula for any N, which applied to N=8 becomes, for the number of “A sets” :
C(56,7) * C(49,7) * C(42,7) * C(35,7) * C(28,7) * C(14,7) / 8! =
56! / ( 7! )^8 / 8! = 42354925592620124113657511548409579520000
… and for the number of “B sets” for each “A set” : (6!)^6 = 139314069504000000
… throwing in the factor of 6! for the permutation of C,D,E,F,G,H and recalling that there are 120 matrix solutions to every “A & B set” specification, we have a grand total of:
509815040933983250324665926101388800612911244378112000000000000
unique 57 card SPOT IT! decks, using the same 57 symbols. And the 57! permutations of the symbols of any one of these will produce 79493377501440 copies of each of them.