That monster is the star, Deneb, familiar in the constellation Cygnus in the northern sky. It is among the brightest stars in the sky, but what cannot be obvious is that it far outstrips its visual rivals in intrinsic brightness, so that it is the bully in our neighborhood. It is a magnitude 1.25 star at a distance of 800 parsecs.

Now, the Sun has an absolute magnitude of 4.83, which is by definition its ideal visual magnitude at a distance of 10 parsecs. So to have a visual magnitude of 1.25, the Sun must appear 10^(.4*(4.83-1.25)) = 27 times brighter than it does at 10 parsecs. That means it must be 1/sqrt(27) times as distant , or about 3.7 parsecs away, or 216 times closer than Deneb, to show the same visual magnitude.

So, conversely, the earth would have to be orbiting Deneb at 216 AU if Deneb were to have the same apparent brightness as the Sun. That’s over five times the distance of Pluto from the Sun, which averages about 40 AU.

The period of an orbiting body is given by M/r^2 ~ r/T^2 or T ~ sqrt( r^3/M ), which embodies Kepler’s third law for a central body of a given mass, but allows us to account for a variable mass. Deneb has about 19 solar masses, so the “year” of this Deneb-earth would be sqrt( 216^3/19 ) = 728 earth years. Well, at least that’s comprehensible!

I was led into these contemplations after having taken the following photograph of Deneb, with its star background in the Milky Way, using my Nikon D5100 mounted on my telescope purely for its use as a “clocked” mount. The exposure is about 20 seconds, so the lack of guidance is not so bad, as long as I get reasonable alignment, for which purpose I have a well practiced system! … ( click to enlarge )

The JPL DAWN mission page has a button for Where is Dawn now?, which is in a drop-down menu if you click on Mission in the main menu on the left of the home page. Dawn of course is the spacecraft that visited the asteroid Vesta, and is now fast approaching Ceres.

If you click on the graphic for Simulated View of Ceres from Dawn you get something like the following screen shot, from Feb 2, 2015

Well, this tells us that it is approaching Ceres, in the middle there, but what stars are those? I couldn’t recognize them, and it was driving me crazy. I thought if I tracked it for a while, I’d see something I recognized, but this got me nowhere.

Note the credit to MYSTIC simulator. This is a tool they hold pretty close to their vest. It is apparently very powerful and used in their actual trajectory planning. Searching for it, I found a link to the NASA/JPL SOLAR SYSTEM SIMULATOR, which is nice, but it provides a much different format, and I was not getting anywhere with it either. Since it was all I could use, I went back a year or so and looked at some wide fields of view, and I was able to track it back to the present, where the background was identifiable as being near the head of Draco, in our Northern sky, but I still had no luck correlating the stars to the MYSTIC image.

The reason for this, I finally realized, is that the SSS tool had not been kept up to date with the latest course corrections ( I presume ) as it gives a different distance from Ceres than MYSTIC, which is official, I guess.

It was finally just dumb luck and persistence that enabled me to spot the correlating stars in my Starry Night software, and I’m sure you’ll agree it’s a good match:

Note that the four stars of the almost-square “box” that Ceres is in ( and remained in for several days, ) is comprised of stars from three different constellations. Two in Serpens Cauda, and one each in Scutum and Ophiucus. A very obscure asterism !

Update: Feb 13

Here’s the latest WIDN image:

Ceres has “moved” ( in line of sight from DAWN ) “southward” ( in celestial coordinates ) into the constellation of Sagittarius. You might recognize the Sagittarian “teapot” asterism directly behind the bottom half of the representation of the DAWN space craft.

Now here’s the funny thing … DAWN is currently almost directly in line with Ceres from our terrestrial POV, as evidenced by this Starry Night view with Chicago set as the viewing location. Ceres is marked, along with it’s orbit. I adjusted the time to make the view align with the WIDN representation, and this view happens to occur at 9:46PM local time, on Feb 13, 2015. ( I did have to turn off the horizon mask, as this view is looking down through the ground at the given hour. Sagittarius rises just ahead of the sun at this season. )

I think this alignment has to be ascribed to coincidence, except that it does mean that DAWN is “rising” towards Ceres along an orbit which is “sunward” of Ceres’ orbit.

Update Feb 19

Here is an animated gif of a loosely spaced sequence of WIDN images, displaced to show a constant star background. This POV definitely gives the impression ( correct, I believe ) that DAWN is rising up through the ecliptic plane as it closes with Ceres. We can see Ceres sinking to the south below Sagittarius. It’s only going to get more interesting!

Feb 20 – A note on escape velocity

The Wikipedia article on Ceres gives a radius of 476 km and an escape velocity of .51 km/sec . This is the speed which gives an object a kinetic energy equal to the negative of the gravitational potential at this distance:

m v²/2 = m GM/R so v²/2 = GM/R

then the escape velocity at some r > R, say, is

v_r = v_R sqrt( R/r ) … very simple!

We note at Feb 20 03:16:52 we have r = 44580 km and v = .082 km/sec

but .51 km/sec sqrt(476/44580) = .053 km/sec

so DAWN is not gravitationally bound to Ceres at this point.

Note that the exact direction of the velocity is not important. Varying the direction just places the object with escape velocity at different places on various parabolic orbits.

Also note that the engine is not firing at this time. It seemed to be in braking mode the last few days, so has it shed any total energy?

On Feb 9 05:06:33 DAWN had r = 107010 km and v = .096 km/sec

The escape velocity at that distance is .51 km/sec sqrt(476/107010) = .034 km/sec

So the fact that it has shed considerable speed shows that it has gotten much closer to gravitational capture. If it were “drifting” it would have gained kinetic energy equal to the difference of the escape velocities at the two distances, requiring …

(v + delta_v )² – v² = .053² – .034²

or v + delta_v = .104 km/sec

One more thing, braking with the same rocket is more effective at higher speeds, and one usually expects that a braking rocket will fire near close approach. The very low thrust of the ion rocket means that the approach has to be more “gentle”, which accounts for the braking having been in progress already. Let’s watch and see if DAWN does pick up a little more speed before the braking resumes, as it must.

… sure enough, DAWN is at 184 mph at Feb 20 13:22:16 vs. 182 mph at Feb 19 23:50:16
Kind of ironic that they give a more precise speed in mph vs. km/s, which is .08 for both times. 1 mph is ( exactly ) .00044704 km/s

Feb 21 – The Approach Begins

Here’s a diagram I drew “by hand” in MS Paint showing the approach of DAWN to “Ceres Space” I started with the MYSTIC graphics for the times shown. I used the given distances and measured the angle of 5 degrees from the background stars, using my STARRY NIGHT software. This gave me the blue line and the close approach distance of a straight line trajectory.

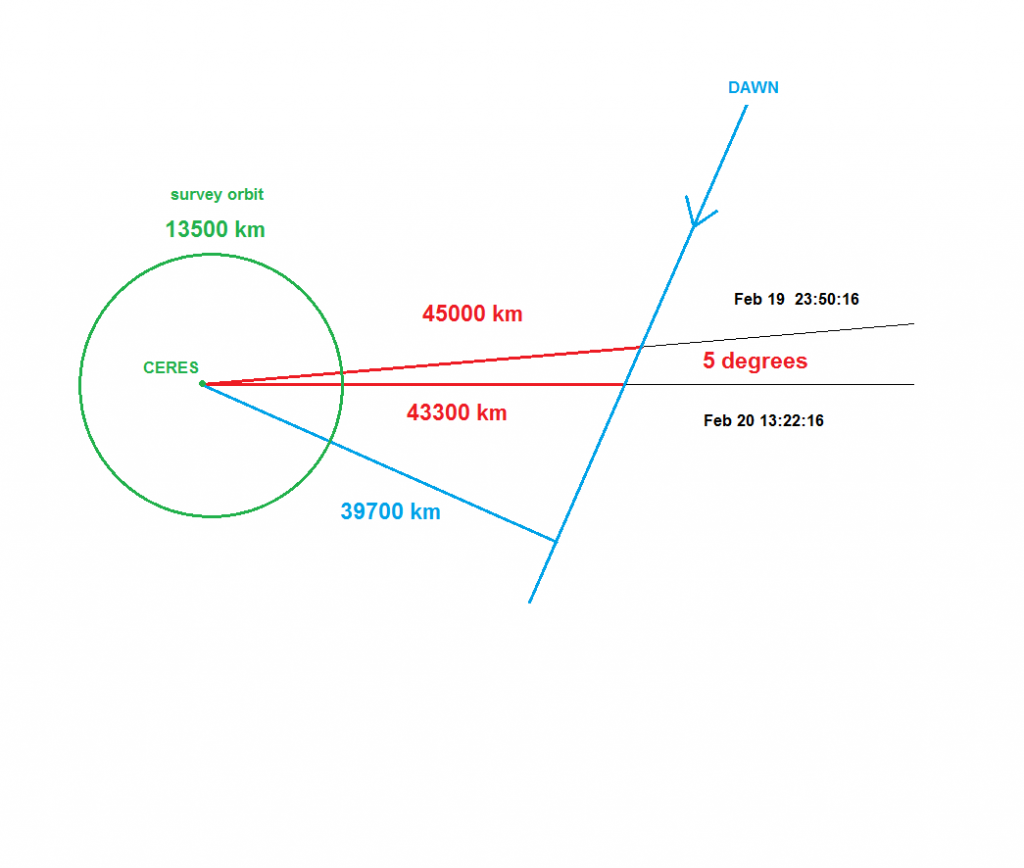
But what about the gravitational attraction of Ceres? It seems that DAWN is not yet bound to Ceres, but it should be on a discernible hyperbolic trajectory.

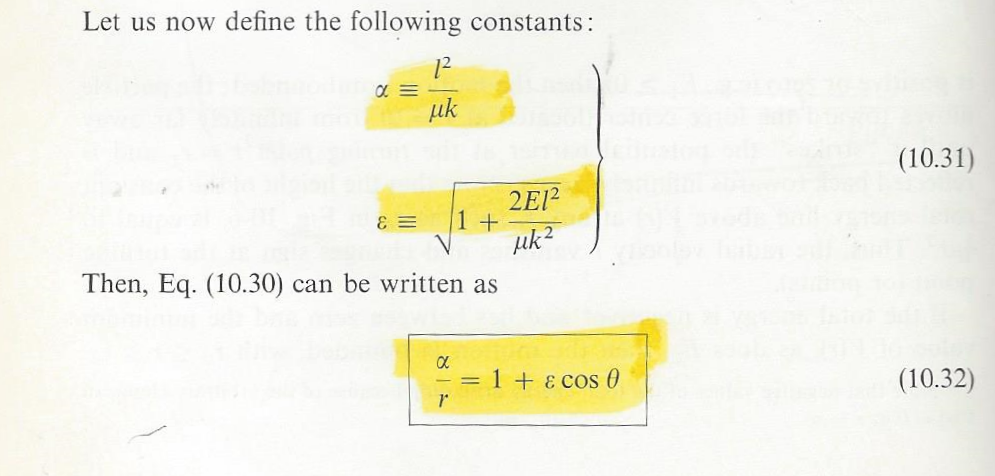
After some thrashing around with pencil and paper, I consulted my old copy of Marion’s CLASSICAL DYNAMICS and found the equation laid out for me, and highlighted to boot!

I used my “hand built” yacc based calculator which features a plug-in definition capability. ( It actually pushes the defining string into the input stream when the defined symbol is encountered. )

Here are the defines I used:

define k “g*R^2”
define l “v*rp”
define alpha “l^2/k”
define E “v^2/2-k/r”
define e “(1+2*E*l^2/k^2)^0.5”

“mu”, for the “reduced mass” can be ignored when one body is much less massive than the other, m << M . Then mu ~= m and it cancels out of the expressions for alpha and e.

k is then GM, but I used GM/R² = g to get k = g R²

Then setting the variables:
g= 0.00028
v= 0.083
rp= 39700
r= 45000
R= 476

( all in kilometers and seconds ) I just typed “alpha” and “e” to get the orbit parameters used in Marion’s equation 10.32, shown above:

alpha
1.71e+05
e
3.46

Then the distance of close approach and the angular displacement from the current position are given by:

alpha/(1+e)
3.84e+04
180/pi * acos( (alpha/r – 1)/e )
35.9

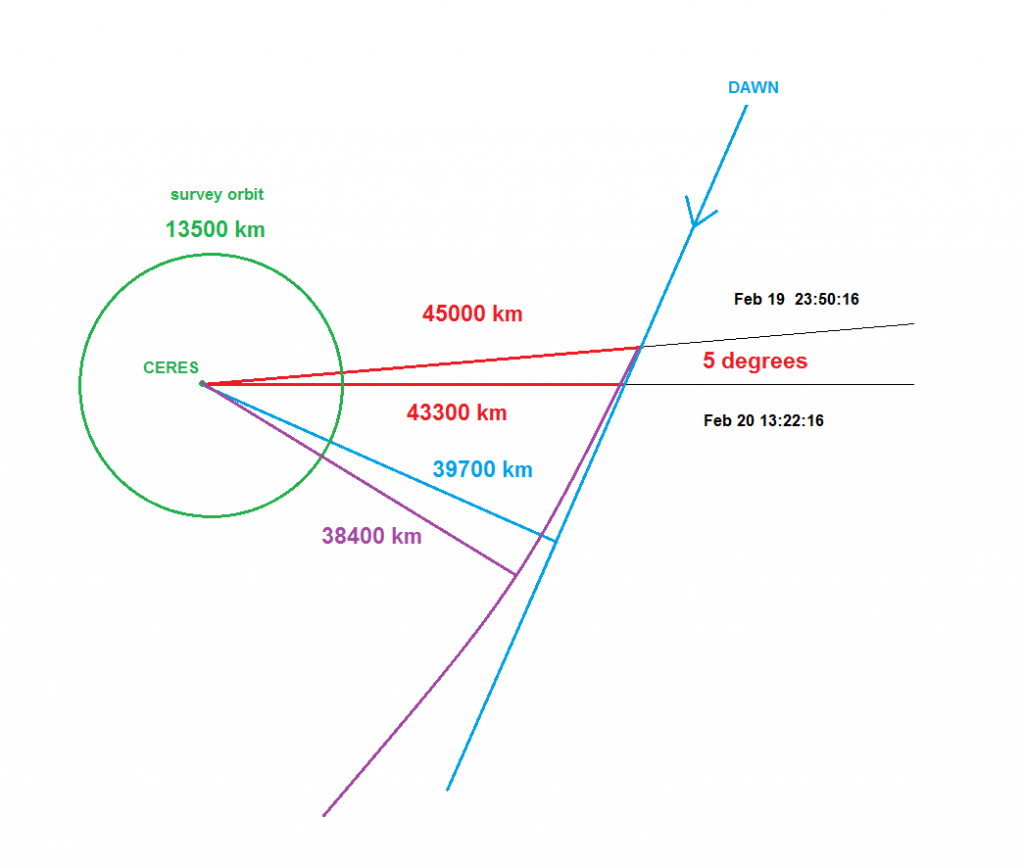
Perhaps surprisingly, these make sense! It says DAWN would approach to 38400 km at an angular displacement of 36 degrees from the current position, assuming it continued to “coast”.

Here’s the result roughly drawn in purple on the diagram. Of course, this is all in the realm of rough estimation!

ARE WE THERE YET ?

… Well, I say we are! According to a definite criterion that I will show you in this most recent animated gif: ( click to see the animation. )

The bright star at top right is Fomalhaut in Piscis Austrinus. It’s actually visible on the southern horizon from mid-northern latitudes, but the POV is shifting to the south. and that’s the constellation Phoenix at the bottom.

But to make my point, I draw your attention to the “Distance to Ceres” caption at the bottom. Note that it “bottoms out” right at 24000 miles, and starts to increase again. DAWN is passing through “periceris” or whatever it might properly be termed. That is, a closest approach to Ceres. Of course, as it continues to “shed energy” it will spiral closer, but right now it is retaining the semblance of an hyperbolic orbit.

As we learned in physics class, the energy of a body at rest infinitely far from a gravitating body is conventionally set to ZERO. If it falls toward a gravitating body it gains kinetic energy but loses potential energy as it sinks into the “gravitational well”. So, any body with net positive energy can escape to infinity with a finite velocity, and is not bound to the gravitating body.

I say all this because the net energy of DAWN ( per unit mass ) is easy to calculate from the MYSTIC captions, and we can gauge its approach to gravitational binding by the steady diminishment that we see in this value, which is equal to 1/2 V_inf², where V_inf is magnitude of the aforementioned “velocity at infinity”.

The value of V_inf was 115 mph in the last frame of the animation at Feb 24 06:33:54 . As of Feb 25 05:34:47, V_inf was down to 107 mph

March 10 – APOAPSIS

The “arrival” or attainment of zero orbital energy, was well noted on March 6, but there was nothing in the motion or actions of the DAWN spacecraft that would have indicated this event, such as it was. It has been “firing” its thruster steadily before during and after this milestone, as it continues to work towards its Survey Orbit. DAWN is now approaching another event, which has a more obvious connection to  its motion. That is apoapsis, as it is generically termed, or maybe apocerium, if we follow Kepler’s coinage of apohelium, which was later “greekified” to the now conventional aphelion.

As an aside, this question of what to call the “apo” point of the orbit has been bubbling along for decades, if not centuries. I only knew of aphelion and apogee, to be honest, but now I’m seeing that apoapsis, that is apo-apsis, is supposed to be the standard term, as awkward as it is. Investigating, I find that apogee derives from apogaeum, a nineteenth century analogue to Kepler’s apohelium, based on gaia, for the earth, I presume.

Of course, I became familiar with apogee from the era of “satellites” in the 50’s and 60’s, when I was quite young. I don’t see why the term can’t be applied to any planetary body, just as one speaks of Martian geology.

Well, at any rate, we are approaching the turning point of DAWN from its continuing motion away from Ceres ( despite it’s inevitable capture ) into a motion falling towards it. Following the Where Is Dawn Now? graphic on the DAWN mission page, we see that its motion is at a low point, suggesting a thrown object at its apex.. In the approximately six hours between Mar. 10,2015 00:03:54 and Mar. 10,2015 06:01:34, DAWN has decelerated from 78 mph to 76 mph, and moved 290 miles further from Ceres; from 43060 miles away to 43350 miles away. These are numbers appropriate to highway driving, not space travel!

So what happens when it “makes the turn” and starts falling towards Ceres ? I anticipate that they will turn off the thruster for a while and let it fall, but we’ll see.

March 17 – Making the Turn

DAWN is still approaching apoapsis, but it is very near, as its speed relative to Ceres of a mere 40 mph would indicate. Here is an animated gif comprised of  1 frame per day for the 14 days March 4 thru March 17. I think you can see a slight bow in the arc of the apparent motion of Ceres against the constellation Orion as DAWN adjusts the plane of its orbit. I did the best I could to keep the star background constant, but its still not perfect, as you can see. I hope it’s good enough to allow you to picture the apparent motion of Ceres against the fixed stars from DAWN’s POV. The sun is almost coming into view just above Orion, as you can see by the almost completely dark disk of Ceres.

Note that the distance from Ceres increases from 55020 km to 77740 km during this interval as DAWN climbs to its apex. You can see the disk of Ceres diminish in size as DAWN recedes from it.

March 25, 2015

On March 19 DAWN achieved apoapsis at 48740 miles from Ceres moving at 34 mph, and is now starting to move closer to Ceres. As of today at 10:33 UTC it has “fallen” to 46460 miles away, and is moving at 40 mph! Here we go!

BTW, DAWN is moving towards a point almost directly opposite the sun from Ceres. WHERE IS DAWN NOW? provides views of the sun ( and other objects ) from DAWN’s vantage point, and here is an overlay showing that the sun is just about to come into view in the Ceres frame of reference … along with the earth and mars too!

Note that I had to expand the “sun view” and slightly rotate it to get a matching overlay.