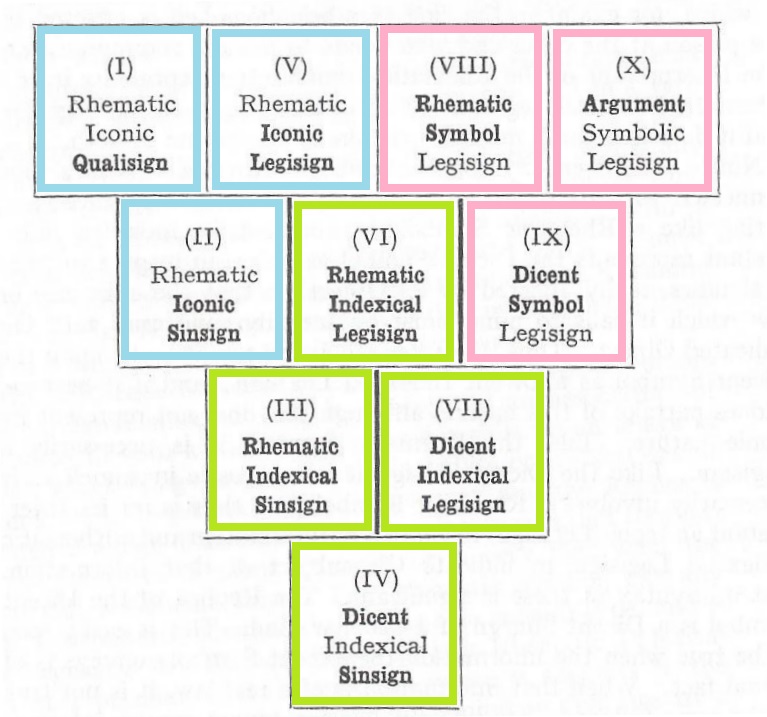
Charles Sanders Peirce, in his essay, LOGIC AS SEMIOTIC: THE THEORY OF SIGNS, presents a diagram displaying the ten types of signs in a triangular array, like bowling pins. These are categorized by three different threefold classifications, his “three trichotomies”, which allow for the specification of 27 types, but only ten are valid. There’s a very simple rule that performs this reduction, but it is not specifically enunciated, that I can notice, even though you can see him applying it.

The Wikipedia article Semiotic elements and classes of signs makes the rule fairly clear with a diagram, but again does not specifically enunciate it, saying simply, ” many co-classifications aren’t found”.

Some years ago, in my own ruminations of the essay I cited, I realized the rule was simply this, that in each label, reduced to a three digit ternary number, abc, where a, b, and c are elements of {0,1,2}, we must have a >= b >= c. Thus when b=0, specifying an Icon, we can only have 000, 100, and 200. The logic of this is that each succesive category can only partake of a quality present in the previous category, so that the Qualisign, 000, is unique, and conversely the Argument, 222, is as well.

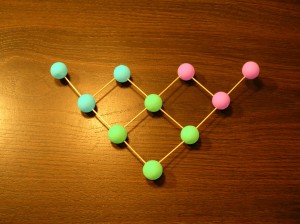
Realizing all this, I made a model representing the subset of the 3X3X3 cube:

This crude model is a number of years old, and its survival is no doubt partly due to its simple construction, as it is composed of exactly two identically folded paper pieces, a reflection of the symmetry of this subset of the cube. It is essentially, except for edge conditions, 1/6 of the cube, as partitioned by 3 bisecting cuts along a major diagonal. I felt that all this symmetry impinged, or ought to impinge on the significance of the categories, but I never pursued such thinking. Nevertheless, the construction does serve as a powerful mnemonic, and stands as a rival to Peirce’s own diagram.

Well, just lately, I had the thought to make a direct comparison of the two, and found that there is a direct relationship, and in fact Peirce’s tableaux does embody most of the symmetry of the cubic model, even if it doesn’t directly display the restrictive rule.

So with that preamble, here is Peirce’s tableaux marked to display the groupings of the Icons, Indexes, and Symbols:

Then here is a new model of the cubic representation using a lattice so you can see all the elements, and of course the same color coding. You can see that the Icons, Indexes and Symbols belong to three separate planes perpendicular to their defining axis:
This is suggestive, but how can we relate this lattice directly to the Tableaux? A start is to try a projection, or view along an axis of symmetry, to spread things out a little. Here is such a view of the same model:
This goes pretty far. Note that the ( green ) Indexical categories do in fact correspond to the Tableaux. ( You may believe me that the correspondence is exact. ) However, the other elements are out of whack. The three rows of this projection are not the same as the rows of the Tableaux.

We can almost rectify everything by flattening the lattice.  This only requires “unbending”  the two right angle connections between the blue and green, and the pink and green:
This is almost it! We have retained the connective character of the lattice model, and come very close to Peirce’s original representation. In fact, we could modify the Tableaux by a simple cut and paste of the Argument and Qualisign elements. But let us bow to precedent and esthetics, and simply swing the lattice elements, which have only one connection, into the “correct” place, and we have an exact correspondence without really sacrificing anything: